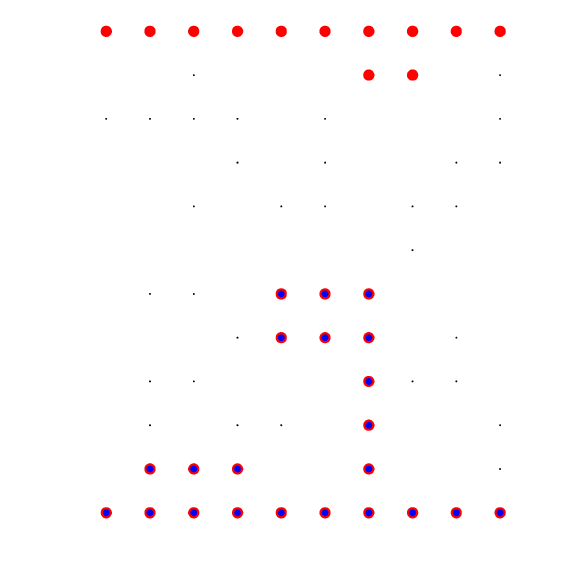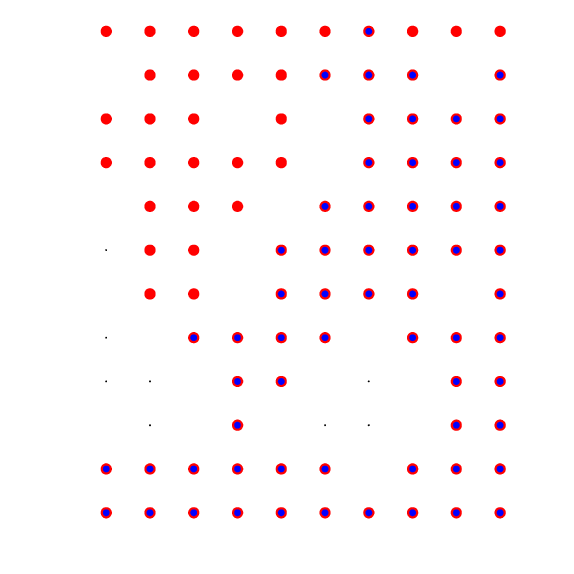Problem 6: Percolation

• Consider a square lattice with N² cells. With probability p put an electrically conducting element in a cell, and with probability q = 1 - p leave the cell empty. Do this for every cell in the lattice.

• When you are done, calculate whether a continuous path for current to flow from the bottom of the lattice to the top exists (current flows up and down, left and right, but not on the diagonals). If so, the lattice is said to percolate.

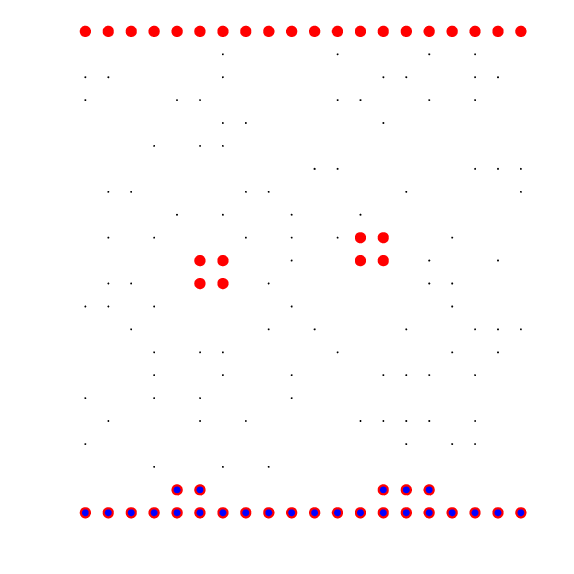
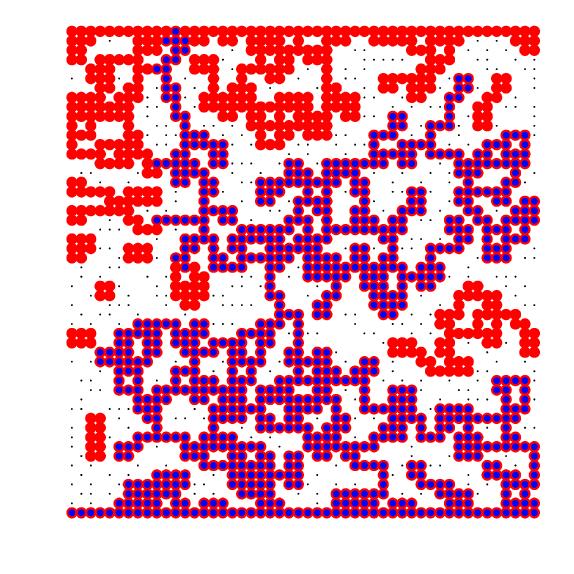
• Test grids - most are coffee, but one is hot chocolate ...

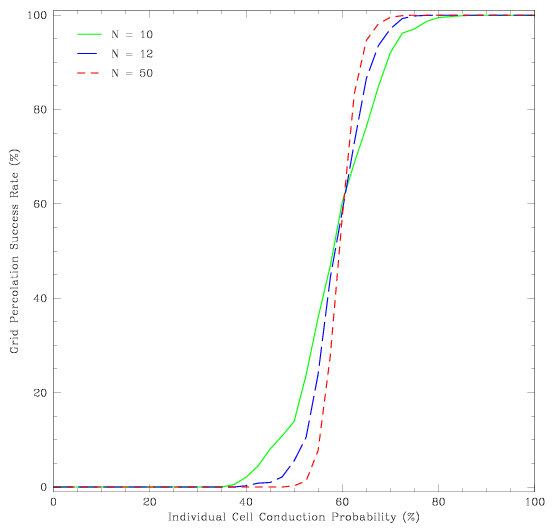
• Evaluate the cases N = {10, 20, 50} and p = {0.1, 0.3, 0.5, 0.6, 0.7, 0.9}. Repeat each of the eighteen cases one-hundred times, and summarize on your findings.

• Sample grids, for various values of N.

• Percolation models are used in the study of epidemics and forest fires, among other topics. The lattice is called a random fractal because of certain invariant properties that it possesses. Percolation is enabled for an individual cell conductivity probability of roughly 60% or greater. The overall probability of percolation does not scale with N - as the grid size increases one might argue that the number of possible conducting paths increases, but this is counteracted by the fact that the path length increases in parallel. N does act to smooth the shape of the peroclation function, however.