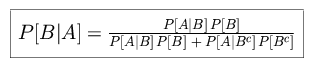
We define
| A | = | the event that the component fails the test |
| B | = | the event that the component is flawed |
| Ac | = | the event that the component passes the test |
| Bc | = | the event that the component is good |
and recall that P[A|B] is defined as the probability of A, given B. Our conditions are that
P[B] = 0.005
We can use Bayes' Theorem to determine the conditional probability (but you should be able to see that this is the correct ratio to consider, from basic principles).
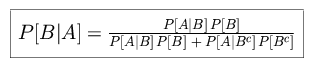 |
Putting in the conditions of our case,
 |
This tells us that only 8.7% of the flagged optics are actually flawed, which is a very high false positive rate.