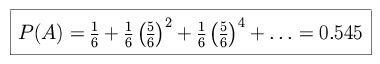
How important is it to go first? How long will the duel last?
The sample space contains all possible outcomes.
| a | = | gun fires for person A |
| b | = | gun fires for person B |
| x | = | gun does not fire |
The duel lasts for k pulls of the trigger, and the gun does not fire for any of the first k - 1 pulls but does fire on the kth pull. The sample points for which A wins are highlighted in red (all of the sample points of odd length).
| a |
| x b |
| x x a |
| x x x b |
| x x x x a |
| x x x x x b |
The probability of A winning the duel can be expressed as follows.
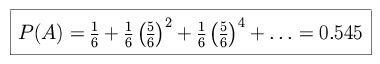 |
Person A thus has slightly better odds of winning than does person B.
We now define D as the duration of the duel (in units of trigger pulls). The average, or expected, value of D is then
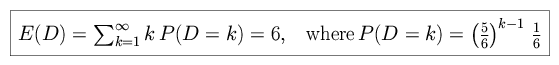 |
Consider the following revision of the rules, if person B complains that he or she has an unfair disadvantage. Suppose that A pulls the trigger once, then B pulls the trigger twice (always spinning the cylinder to a random position between firings), then A pulls the trigger three times, then B four times, and so forth.