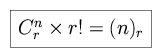
The general formula for the number of subpopulations C_rⁿ of size r in a population of size n can be derived as follows. Consider an urn containing n distinguishable balls. The number of ordered samples of size r is (n)_r. For each subpopulation of size r, there are r! different arrangements, and therefore r! different ordered samples. Thus for C_rⁿ subpopulations there must be C_rⁿ × r! different ordered samples of size r.

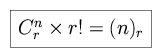We define the binomial coefficient C_rⁿ as follows.

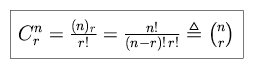with the clear consequence

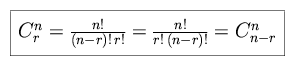Consider a sample of size n. The sample description space is 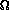= {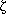₁, ..., 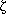_n}. Each descriptor 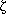_i is either present or not present in an arbitrary subset, so the number of distinct, non-ordered subsets is 2ⁿ. From this we conclude that
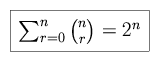