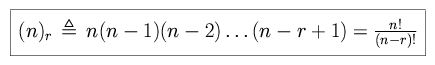We define a population of size n to be a collection of n elements without regard to order. Two populations are considered to be different if there exists at least one element which is contained in one but not contained in the other.

A subpopulation of size r from a population of size n is a subset of r elements taken from the complete set of n. Two subpopulations are considered to be different if there exists at least one element which is contained in one but not contained in the other.

Consider a population of n elements a₁, a₂, ... a_n. Any ordered arrangement a_k1, a_k2, ... a_kr of r elements is called an ordered sample of size r.

Consider now an urn containing n distinguishable, numbered balls. We remove balls one by one from the urn. How many different ordered samples of size r can be formed?

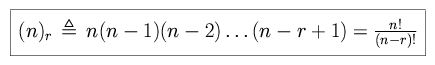• Sampling with replacement: After each ball is removed, its number is recorded and it is returned to the urn before a ball is again selected. There are always n balls which can be selected, and so there are n^r different ordered samples of size r which can be formed.

• Sampling without replacement: After each ball is removed, it is not replaced in the urn. There are n balls which can be selected for the first sample, n - 1 balls for the second sample, and so forth. We conclude that for a population of n elements, there are

• The number of subpopulations of size r in a population of size n: For a sample of 6 balls,
  • The number of ordered sets that can be formed with replacement is 36.
  • The number of ordered sets that can be formed without replacement is 30.
  • The number of sets of size 2 that can be formed is 15 (order does not matter).