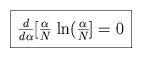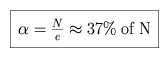Selecting the Best Puppy
Your goal is to select a puppy, given the following constraints.
- Sample Size - There are N puppies available for adoption.
- Random Order - The N puppies will be presented to you in a random order.
- Instantaneous Choice - You see each puppy once and only once,
and must decide at that time whether or not to adopt her. If you
decide not to adopt a given puppy, she goes immediately off to a home
somewhere else. If you do decide to adopt a given puppy, you will not see any
more candidates.
Let us first consider the case of an infinite number of puppies. A good
working strategy (a wait and see algorithm) is to look at enough
puppies to develop a sense of the range available, and then to select the first
puppy which exceeds this range. We assume that puppy qualities can be
combined into a single quantity, and that all N candidates could be sorted
from 1 (least acceptable) to N (best match to your requirements).
Restating this mathematically, for a finite number of puppies, we first
observe  puppies. The best will
be ranked
puppies. The best will
be ranked 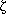 , where puppy ranks can
range from 1 to N. We then select the next puppy which is ranked higher than
, where puppy ranks can
range from 1 to N. We then select the next puppy which is ranked higher than
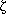 . Our goal is to determine a
best value for
. Our goal is to determine a
best value for  .
.
We define Cm( ) as
the event that the largest number drawn from the first m draws will appear in
the first
) as
the event that the largest number drawn from the first m draws will appear in
the first  draws.
draws.
Let X be the draw of the best suited puppy. We require that two conditions
be met, in order to select this candidate.
The puppy with the largest rank which is drawn before the best
puppy, X, is drawn must lie within the survey group, not after it but
before X. We thus require {X =  + j + 1} and C
+ j + 1} and C +j(
+j( ), for 0
), for 0  j < N. We can restate the first
condition as follows.
j < N. We can restate the first
condition as follows.
The total condition is then
The probability of making the correction decision is
We can convert the sum into an integral, and use a simple variable
substitution to solve it.
We maximize P[D] where the slope is unity with regards to  , and use the chain rule and
integration by parts to determine
, and use the chain rule and
integration by parts to determine
Therefore, we maximize the probability of selecting the puppy best suited
to our requirements if we select the best one that we see after first
surveying roughly one-third of the pool.
 puppies. The best will
be ranked
puppies. The best will
be ranked 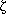 , where puppy ranks can
range from 1 to N. We then select the next puppy which is ranked higher than
, where puppy ranks can
range from 1 to N. We then select the next puppy which is ranked higher than
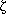 . Our goal is to determine a
best value for
. Our goal is to determine a
best value for  .
.
 puppies. The best will
be ranked
puppies. The best will
be ranked 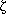 , where puppy ranks can
range from 1 to N. We then select the next puppy which is ranked higher than
, where puppy ranks can
range from 1 to N. We then select the next puppy which is ranked higher than
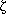 . Our goal is to determine a
best value for
. Our goal is to determine a
best value for  .
.
 ) as
the event that the largest number drawn from the first m draws will appear in
the first
) as
the event that the largest number drawn from the first m draws will appear in
the first  draws.
draws.
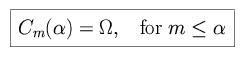
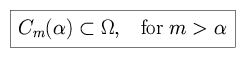

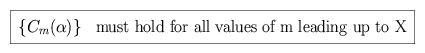
 + j + 1} and C
+ j + 1} and C +j(
+j( ), for 0
), for 0  j < N. We can restate the first
condition as follows.
j < N. We can restate the first
condition as follows.
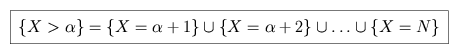
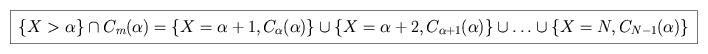
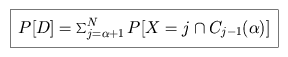
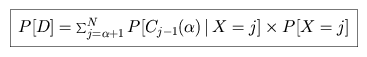
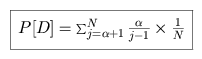

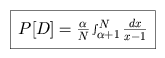

 , and use the chain rule and
integration by parts to determine
, and use the chain rule and
integration by parts to determine