We can easily determine all of the possible outcomes of the experiment, by denoting the birth of a male puppy as {0} and the birth of a female puppy as {1}. With four puppies, the options are {0/1} x {0/1} x {0/1} x {0/1}, with sixteen possible outcomes. We can express these as binary numbers.

0 = 0000	4 = 0100	8 = 1000	12 = 1100
1 = 0001	5 = 0101	9 = 1001	13 = 1101
2 = 0010	6 = 0110	10 = 1010	14 = 1110
3 = 0011	7 = 0111	11 = 1011	15 = 1111

where the blue numbers have a split of [4 - 0], the green numbers have a split of [3 - 1], and the red numbers have a split of [2 - 2]. Counting up our sequences, we see that there are 2 / 16 = 1 / 8 ways to have four of either gender, 8 / 16 = 1 / 2 ways to have three of one gender and one of the other, and 6 / 16 = 3 / 8 ways to have two of each gender.

Alternatively, we can treat the experiment as a series of Bernouli trials. A Bernouli trial is defined by two conditions: first, successive trails are indepenent of each other, and second, each trial has precisely two possible outcomes.

For n puppies, with probability p of a female puppy and 1 - p of a male puppy, the probability of k females and n - k males is

For the case of the puppies, n = 4 and p = 1/2.
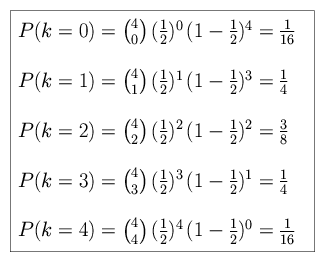