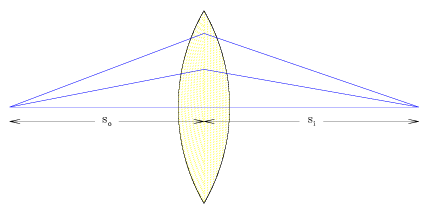
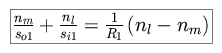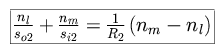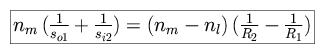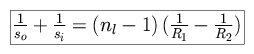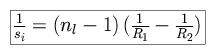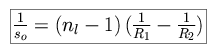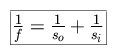The Thin-Lens Equation
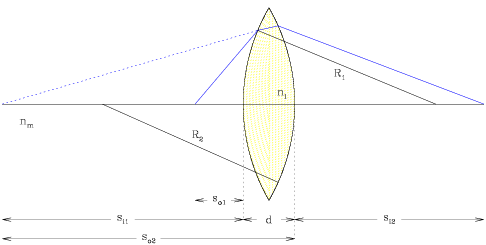
Consider the case of a thin lens, created by grinding off the second side
of a spherical surface. We begin by deriving the relationship between between
the path of incident and twice refracted light from an initial medium of index
of refraction nl through a thin lens with radii of curvature
R1 and R2 and index of refraction nm.
 |
| [NMSU, N. Vogt] |
For the first surface of refraction, we use the results of our analysis of
refraction through a spherical surface.
The second surface "sees" the light transmitted through the lens as
incoming light from the virtual image located at so2.
We can use the fact that |so2| = |si1| + d, and
combine the two equations of refraction to obtain the following.
 |
| [NMSU, N. Vogt] |
For the case of air, this is the lenmaker's formula.
For the case of an object at an effective distance of infinity, this simplifies to
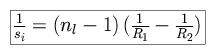 |
 |
| [NMSU, N. Vogt] |
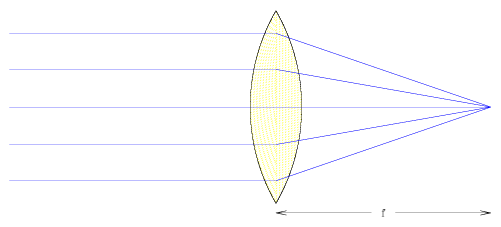
For the case of an object imaged at infinity, this simplifies to
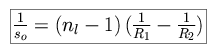 |
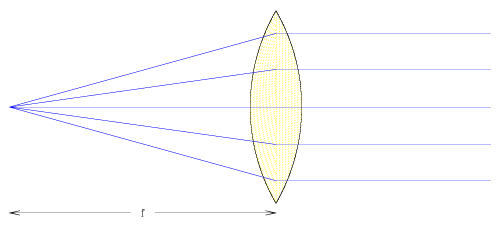 |
| [NMSU, N. Vogt] |
where we define the thin-lens formula
A complete derivation was presented during lecture.