
 = frequency, radians/second
= frequency, radians/second = frequency, seconds-1
= frequency, seconds-1 /
/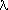 = wavenumber, radians/Angstroms
= wavenumber, radians/Angstroms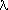 = wavelength, Angstroms
= wavelength, AngstromsWe can visualize lights in the form of discrete particles, when the wavelength of the light is smaller than the physical scale of the optics. This is the regime of geometrical optics.
We can visualize light in the form of a electromagnetic wave, when the wavelength of the light is larger than the physical scale of the optics. This is the regime of diffraction optics. We say that such light is emitted in a spherical distribution from a point source, and we define a wavefront as a surface across which the phase of the light is a constant. The wavefront will propagate as a function of time and of position.
| I = Io ei (wt + kr) | w = 2  = frequency, radians/second = frequency, radians/second |
 = frequency, seconds-1 = frequency, seconds-1 |
|
| t = time, seconds | |
k = 2 / /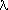 = wavenumber, radians/Angstroms = wavenumber, radians/Angstroms |
|
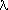 = wavelength, Angstroms = wavelength, Angstroms |
|
| r = distance, Angstroms |
 |
| [NMSU, N. Vogt] |
When we examine a small angular fraction of a set of spherical wavefronts, we can approximate them as parallel lines. One example of this is the light emitted from a source at a great distance, collected by a set of telescope optics.