How Bright is the Sun?
The brightness of the Sun is inversely proportional to our distance from it
(the further way from it we are, the fainter it appears to be). It varies
with the square of the distance. Thus we say that its brightness follows an
inverse square law.
| Light Dims with Distance |
 |
| (click on picture for animation) |
Consider rays of light emitted from the Sun. You can see that as the rays
move away from the Sun, they spread farther and farther apart from each other.
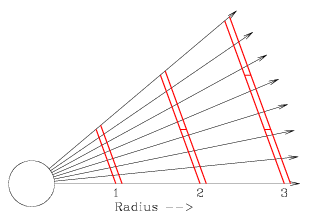
Let us examine the light coming from a small piece of the Sun, as shown
below. We have marked along the horizontal axis points at 1, 2, and 3 units.
These could represent the position of the Earth relative to the Sun, and then
positions that are twice and three times as far away. The red lines show the
length needed to span the separation between the end sunbeams at each radius.
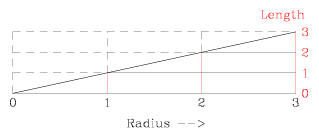
Now we explore the relationship between the radius, the distance we lie
away from the Sun, and the length needed to span the separation between end
sunbeams. This is a linear relation. This means that if we double the
radius, the length increases by a factor of two. If we triple the radius, the
length increases by a factor of three. This shows us that as we move from a
radius of 1 to a radius of 3, it will take a length three times longer to
encompass a single set of sunbeams.
 |
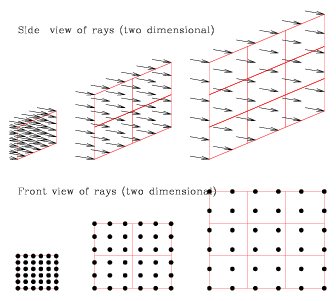
This means that the spacing between neighboring sunbeams will increase by
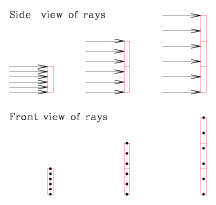
a factor of three. The figure below shows a set of sunbeams hitting a surface
at a radius of 1, 2 and 3 from the Sun. The side view shows the light coming
from the left and hitting the surface at the right, while the front view shows
the light shining out of the page directly towards us. We can see that a unit
length of ground will receive 6 sunbeams at a radius of 1 (left), 3 sunbeams
at a radius of 2 (middle) and 2 sunbeams at a radius of 3 (right). Another
way to say this is that the intensity of the light will fall off inversely
with radius.
 |
The final figure is the same, only it shows the sunbeams falling on a
surface with width and length rather than just length. This is equivalent to
a patch of land on the surface of the Earth. The side view shows the light
coming from the left and hitting the surface at the right, while the front
view shows the light shining out of the page directly towards us. We can see
that our unit patch of ground will receive 6 × 6 = 36 sunbeams at a radius
of 1 (left), 3 × 3 = 9 sunbeams at a radius of 2 (middle) and 2 × 2 =
4 sunbeams at a radius of 3 (right). Another way to say this is that the
intensity of the light will fall off inversely with the square of the
radius.