Summary of results:

Maria Mitchell's score on this quiz was 40% (any incorrect choices are highlighted in red).

#1. This equation shows that the ratio of how much energy we observe from two stars (E/E) can be calculated from their difference in magnitudes. If two stars differ by 2.0 in magnitude, how many times brighter is the brighter one than the fainter one?

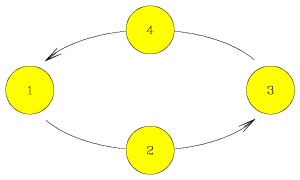
#2. The first figure below shows the roughly circular orbit of a star within a spectroscopic binary system (with a stellar companion too faint to see), and the second figure plots the measured velocity of the star over time. At the time at which the velocity corresponding to the red point was measured, the star was           .

#3. As a newly formed stellar cluster begins to age, the number of giant stars           

#4. If a clock on Earth runs more slowly than a clock in outer space by 2 parts in a billion (2 × 10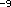), how many years would it take for two such clocks to disagree by a day?

#5. Imagine three galaxies A, B, and C, placed in a one dimensional universe as shown below. If the universe doubled in size, how far would galaxy C be from galaxy A?

Elapsed Time: 24.75 minutes

#1. This equation shows that the ratio of how much energy we observe from two stars (E/E) can be calculated from their difference in magnitudes. If two stars differ by 2.0 in magnitude, how many times brighter is the brighter one than the fainter one?

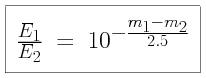
Write your answer in the box, using a standard format for numbers. For example, if one star is 150 times brighter than the other type "150" or "1.5e2".

We know that a change of one magnitude is equal to a factor of 2.51 in brightness, and a change of five magnitudes is equal to a factor of 100 (2.51 × 2.51 × 2.51 × 2.51 × 2.51) in brightness. A change of two magnitudes is equal to a factor of 2.51 × 2.51, or 6.31.

We can calculate this explicitly using the equation connecting magnitudes to observed energies. For the case where m – m = 2.0,

E

E

E

      

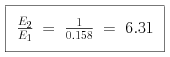
#2. The first figure below shows the roughly circular orbit of a star within a spectroscopic binary system (with a stellar companion too faint to see), and the second figure plots the measured velocity of the star over time. At the time at which the velocity corresponding to the red point was measured, the star was           .

at position 1	well past position 1, but not yet at position 2
at position 2	well past position 2, but not yet at position 3
at position 3	well past position 3, but not yet at position 4
at position 4	well past position 4, but not yet at position 1

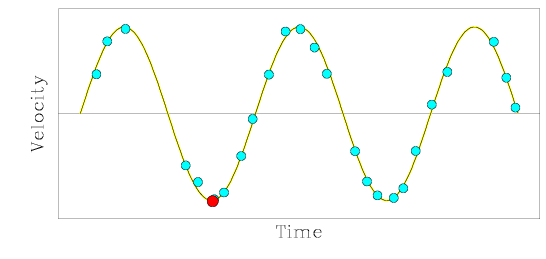When the star lies at position 2 or position 4, it moves from left to right or from right to left across the page. Its spectra will thus show stellar absorption lines for elements such as hydrogen, helium, calcium, iron, and magnesium at their expected rest wavelengths. At position 1 the star will be moving toward us, so its spectral features will be blueshifted to shorter wavelengths and it will have a negative velocity. At position 3 the star will then move away from us, creating redshifted spectral features at longer wavelengths, as the star will have a positive velocity.

In summary, the star will have a maximum positive velocity at position 3, and a maximum negative velocity at position 1, and will display no velocity at positions 2 and 4. When it is transitioning from one of these positions to the next, it will exhibit a transitional, average velocity. As the star currently exhibits its maximum negative velocity, it must lie at position 1.

      

#3. As a newly formed stellar cluster begins to age, the number of giant stars           

decreases	increases
remains constant	varies unpredictably

Over time, stars run out of hydrogen fuel and shift from the Main Sequence into the giant phase.

      

#4. If a clock on Earth runs more slowly than a clock in outer space by 2 parts in a billion (2 × 10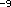), how many years would it take for two such clocks to disagree by a day?

Write your answer in the box, using a standard format for numbers. For example, if your answer is four thousand years type "4000", or "4e3".

A clock on the surface of the Earth will run more slowly than one in outer space due to the surface gravity, by two parts in a billion. This means that for every second counted off on the clock in space, the Earth clock will count 1 second plus 2 × 10 seconds.

How many seconds must elapse before those little 2 × 10 seconds of extra time sum to a full second? We need to wait 5 × 10 seconds, as (2 × 10) × (5 × 10⁸) = 1. So in 5 × 10 seconds, our two clocks will report times which differ by a second. There are 60 seconds in a minute, 60 minutes in an hour, and 24 hours in a day. We thus need to wait 60 × 60 × 24 times as long for them to disagree by a full day, or 60 × 60 × 24 × (5 × 10 seconds) = 4.32 × 10 seconds.

That's a lot of seconds, so let's convert that value into units of years. Remembering that there are 60 × 60 × 24 × 365 seconds in a year (or for convenience, × 10 seconds in a year), 4.32 × 10 seconds is equal to (4.32 × 10 seconds) / ( × 10 seconds per year) = 1.38 × 10 years = 1.38 million years!

      

#5. Imagine three galaxies A, B, and C, placed in a one dimensional universe as shown below. If the universe doubled in size, how far would galaxy C be from galaxy A?

100 units	300 units
500 units	1000 units

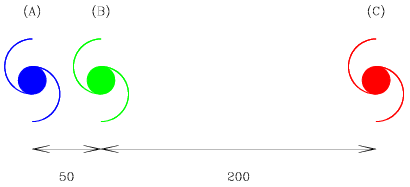
When we say that the Universe itself is expanding, we mean that every part of space is expanding away from every other part of space. If the Universe doubles in size then a length of 50 units will stretch to 2 × 50 = 100 units, while a length of 200 original units will stretch to 2 × 200 = 400 units. Every point is space is moving further away from every other point in space.