When a massive star collapses into a dense neutron core, the angular momentum of the entire star is forced into a much smaller structure. Like an ice skater who pulls her arms inward when spinning, this causes that star's rotation to speed up tremendously (up to almost 1,000 times per second).
Neutron stars have strong magnetic fields, and we can detect the radiation emitted from the poles (which point up and down along one axis, rather like the North and South poles of the Earth). But because the magnetic poles of a neutron star are not aligned with its axis of rotation, as the star spins the radiation will spin in and out of our field of view (pointing toward and then away from us).
This causes the neutron star to pulse on and off in a regular, periodic sequence, and gives it the name pulsar (short for pulsating star). We know the relationship between the period of pulsation and its frequency, namely
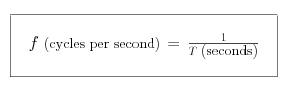
so we can calculate the frequency, in cycles per second, from the period, in seconds. They are inversely related. If the pulsar period increases then there is more time between successive pulses, and the frequency decreases. If the pulsar period decreases, the pulses will arrive closer together, and the frequency of pulsation will increase.
When comparing the periods of two pulsars, we can determine their relative frequencies without calculating them explicitly. We know that if the period of a pulsar increases its frequency decreases, so if we compare a shorter period and a longer period pulsar, which one will spin at a higher frequency?