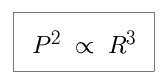
Kepler's third law tells us that there is a set relationship between the amount of time it takes any planet to orbit once around the Sun (the local year) and the distance it lies from the Sun (the radius of its orbit). Simply put, the square of the period P is is proportional to the cube of the orbital radius R.
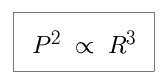
We take the square root of both sides of Kepler's Third Law to find the period.
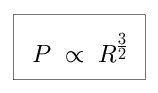
We know that the Earth has an orbital radius of 1 A.U., and takes one Earth year to go once around the Sun. Given these values, we can determine the rotational period of any other planet once we know its orbital radius. The period, in Earth years, is equal to the radius, in Earth orbital radii, raised to the power of 1.5.
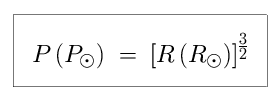
Imagine that we discovered a planet which lay twice as far from the Sun as the Earth does, at an orbital radius of 2 A.U. How long would a year last on this planet?
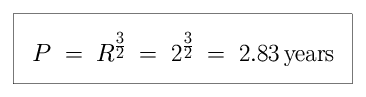
If twin children grew up, one on Earth and one on the new planet, how would their ages differ? When the Earth child reached an age of 21 years, the twin would still be less than eight (local) years old!
Now imagine that we found a planet which took 10 years to orbit the Sun. How far from the Sun would it be? We can simply invert our equation, solving for R rather than for P.
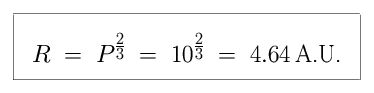
This planet would lie almost five times as far from the Sun as the Earth does, making it a fairly chilly piece of real estate!
To convert our radius from A.U. (the average distance between the Earth and the Sun) and kilometers, we simply multiply by the number of kilometers in one A.U.

You may wonder what is controlling the relationship between period and radius. As is often the case, the underlying cause of the relation is gravity. The gravitational attraction of the Sun pulls the planets inward, and only the kinetic energy with which they spin around the Sun keeps them from being subsumed. This gravitational attraction scales with the mass of the Sun (more mass being equivalent to a more powerful attractor), and the distance to the planet (objects closer to the Sun are pulled in more strongly).