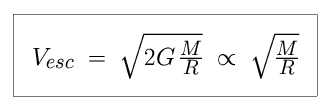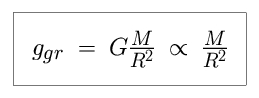
Suppose you wanted to place a new satellite into orbit around the Earth. You might first try to do this by throwing your satellite (let's say it's a baseball) up into the air. You would quickly see your baseball fall back to Earth and break someone's window (oops!). What could you do to cause it to go higher? If you threw your baseball faster it would go higher into the air, but it would still turn around and come back to ground. Even if you had a Major League Baseball pitcher throw your ball into the air at over 100 miles per hour, it would only manage to get about 100 meters in the air (334 feet).
How fast would you have to throw your baseball so that it flew up into the air and away from the Earth, never to return? You would need to throw it at a speed of 11 kilometers per second; that's about 24,500 mph !!!
This limit, the speed necessary to escape the influence of an object's gravitational attraction, is called the escape velocity.
The gravitational pull of an object is a function of both its mass and its size. The more massive it is, the stronger its attraction. The smaller the size of that mass (or the more dense the object is), the stronger the gravitational force will be on its surface. For an object of mass M and radius R, we say that the gravitational force at the surface is
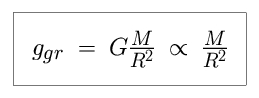
The expression for the escape velocity V is quite similar. In essence, the Earth's gravity creates a gravitational well; the stronger the gravitational force, the deeper the well, and the more energy it takes to climb out of it.