There are two types of waves that we will study, waves propagating over a distance, and waves propagating through time. An ocean wave is a fine example of both types of waves.

A Wave Traveling Through Space
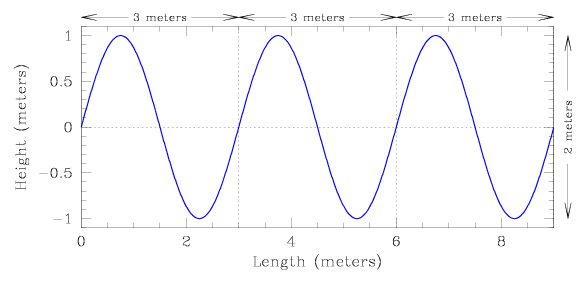
Consider first a wave which propagates over a distance. If you stand on a pier above the ocean and watch the waves roll into the shore, you can observe that at any instant the water forms a wavelike shape, with a steady progression of peaks and dips as you move from the shore outward toward the sea. In the example shown below, the water would be at its lowest height (the nadir) 2.25 meters, 5.25 meters, and 8.25 meters from shore, and would be at its highest (the peak) 0.75 meters, 3.75 meters, and 6.75 meters from shore.

For a wave traveling through space, we examine how it rises and falls over a distance, at a particular instant in time. We can characterize the behavior of the wave as follows.

• Wavelength
  The wavelength of the wave is simply the distance (the length) over which the wave goes through one complete cycle, or pattern. The wave shown below starts at a height of zero meters, goes up to one meter, then down to minus one meters, and returns to a value of zero meters, all within a distance of three meters. The figure shows three complete wavelengths (with three peaks, and three dips), or three complete repetitions of the pattern.

• Amplitude
  The amplitude of the wave is the difference between the highest point and the lowest point along the wave. We say that the wave shown below has a peak-to-peak amplitude of two meters.

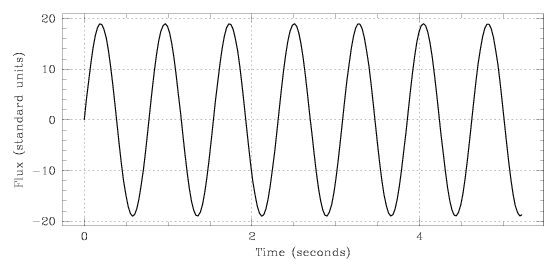
A Wave Traveling Through Time
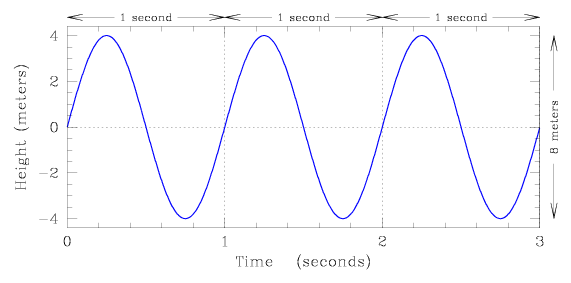
Consider second a wave which propagates through time. If you stand on a pier next to a particular fencepost and watch the waves roll into the shore, you can observe how the water that passes your fencepost forms a wavelike shape, with a steady progression of peaks and dips passing toward the shore. In the example shown below, the water would be at its lowest height (the nadir) after 0.75 seconds, 1.75 seconds, and 2.75 seconds, and would be at its highest (the peak) after 0.25 seconds, 1.25 seconds, and 2.25 seconds.

For a wave traveling through time, we examine how it rises and falls over time, at a particular position in space. We can characterize the behavior of the wave as follows.

• Period
  The period of the time-domain wave is analogous to the wavelength of the spatial wave. It is simply the amount of time over which the wave evolves through one complete pattern of rises and dips (a full cycle). The wave shown below starts at a height of zero meters, goes up to four meters, then down to minus four meters, and returns to a value of zero meters all within a single second. The figure shows three complete wavelengths (with three peaks, and three dips), or three full periods.

• Frequency
  The frequency of the wave is the inverse of the period. If the period is the amount of time it takes for the wave to complete a full cycle, then the frequency is the number of cycles which fill a single time unit. A wave with a period of 30 seconds thus has a frequency of 1 ÷ 30 = 0.033 cycles per second, or 0.033 Hertz (Hz). A much faster wave with a period of 0.4 seconds repeats 2.5 times per second, and has a higher frequency of 1 ÷ 0.4 = 2.5 Hz.
  

• Amplitude
  The amplitude of the wave is the difference between the highest point and the lowest point along the wave. We say that the wave shown below has a peak-to-peak amplitude of eight meters (imagine surfing on this wave!).

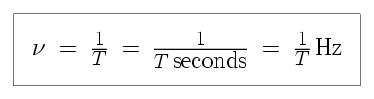
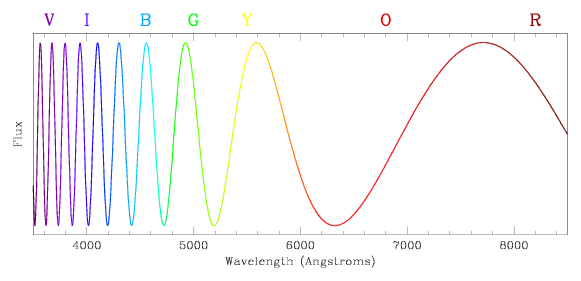
Visual Light Waves
For a wave of light with a wavelength between 3800 and 7400 Angstroms, we can connect the wavelength to a color as perceived by our eyes. The shortest, bluest wavelength light that we can see lies at about 3800 Angstroms (one Angstrom is one hundred millionth of a centimeter), and the reddest light we can perceive has wavelengths of roughly 7400 Angstroms. The next figure shows how the wavelength correlates with the color of the light.

We like to use blue and red as the end points of this plot, and so we say that green light is redder than blue light (which just means that green light has a longer wavelength than blue light), yellow light is redder than green light, and red light is reddest light of all. Similarly, red light is the least blue, orange light is bluer than red light, yellow light is bluer than orange light, green light is bluer than yellow light, and blue and violet light are the bluest of all the colors that we can see.

Measuring with Accuracy
It is important to make measurements as carefully as possible, when reading from a figure. Here are a couple of tricks to help you to do this as easily as possible.

• Measure Multiples
  If we want to measure the period of the wave shown below, we can take advantage of the fact that six full periods are shown on the figure to improve the accuracy of our measurement. Let us assume that we can measure the position of a point at which the wave function crosses the y-axis (where it has a value of zero) to within 0.05 seconds (one-tenth of the interval between the smaller tick marks on the x-axis).

  If we attempt to measure the crossing point after a single period, we get a value of P = 0.70 ± 0.05 seconds. Our value has fairly large error bars, ranging from 0.65 to 0.75 seconds. But what if we instead measure the crossing point after six periods have passed? We now get a value of 6 × P = 4.6 ± 0.05 seconds. To determine the length of one period from this measurement, we divide by a factor of six and get P = 0.77 ± 0.008 seconds. The error has dropped by a factor of six!

  
  The period of this wave is in fact 0.77 seconds, so you can see that by making a smarter measurement we were able to improve our accuracy.

• Leverage Labels
  When estimating the relative amplitude of two waves, read as much information as you can from the labels. In the figure shown below, both wave functions have a peak-to-peak amplitude of roughly 175 standard units. Which one has the higher amplitude?

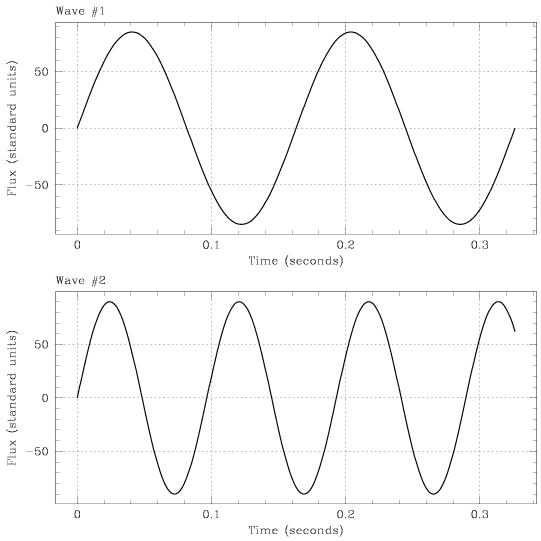
  This may seem a difficult choice if you attempt to make an absolute measurement of the amplitude of each wave. But we don't need to measure the exact height of each wave – we just need to know which one goes higher than the other.

  Take a close look at the tick marks along the y-axis. Both plots have the 50 mark identified with a 50, and then have four small tick marks above indicating the positions of 60, 70, 80, and 90 standard units. On the top plot, there is very little extra space above the 90 tick mark. On the bottom plot, however, there is a lot of space above the 90 tick mark (the bottom plot goes almost all the way to 100 standard units). This tells us that Wave #2 must have a slightly higher amplitude than Wave #1, because it forced the y-axis to extend to a slightly larger value.

  
  The amplitude of Wave #1 is 170 standard units, versus 180 for Wave #2, so our technique is confirmed.