A radioactive half-life is the amount of time it takes for half of the atoms in a sample of a given radioactive element to decay, changing from an unstable form into another state. During the initial half-life, twice as many atoms will decay as during the second half-life. During the second-half life twice as many atoms will decay as during the third half-life, etc.
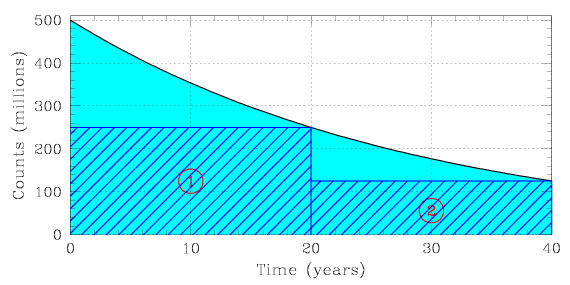
When determining the half-life of a radioactive sample based on a plot of its decay rate, divide the total count rate (the number of atoms) for that sample by two. Draw a horizontal line at that value on the y-axis (the vertical axis). At the point where your line meets the plotted curve, draw a vertical line down to the x-axis (the horizontal axis). The value at which your vertical line meets the x-axis will tell you the amount of time that elapsed during a single half-life.
In the figure shown below, we begin with a total number of 500 million atoms. We draw a horizontal line at a height of 250 million, extend it over to the right, and observe that the sample decreases from 500 to 150 million radioactive atoms over a time period of 20 years. Repeating the process for a second half-life, we confirm that in another 20 years the sample decreases from 250 to 125 million radioactive atoms.

Keep in mind that the atoms which decay do not disappear into thin air – they are merely converted into another element or isotope.