The Hertzsprung-Russell Diagram

Stellar Radii

We can use Stephan's Law, a relation from the physics of the 19^th century, to figure out the sizes of stars. If E is the energy radiated away from the star (luminosity) in the form of electromagnetic radiation, T is the surface temperature of the star, and is a constant known as the Stephan-Boltzmann constant, then

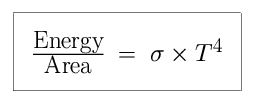This means that if you double the temperature of an star, it will radiate 2 x 2 x 2 x 2 = 16 times as much energy per square unit of area, and also in total if its surface area doesn't change.

Now let's consider the case of two stars, the Sun and alpha

Ori. We define the subscripted symbol

to mean that of the Sun. Thus the Sun has a luminosity of 1 L (1 L = 3.9 × 10

ergs per second), and a temperature of 1 T (1 T = 5,800 K).

Star Luminosity (L) Temperature (K)

Sun 1 5,800

alpha Ori 27,000 3,400

Star	Luminosity (L)	Temperature (K)
Sun	1	5,800
Ori	27,000	3,400

Something strange is happening here! The Sun has a higher surface temperature, so it must radiate more energy per unit surface area than alpha Ori. In spite of this, alpha Ori has a far greater luminosity than the Sun! There is only one way that alpha Ori could radiate more total energy – it must have a larger total surface area.

How much larger is Ori than the Sun? The energy per unit area for the Sun is larger than that of Ori by :
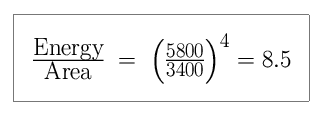If the two stars had the same radius and surface area, the Sun would radiate 8.5 times as much energy. But Ori radiates 27,000 times more energy than the Sun.
We can quantify the difference in the size of the two stars using Stephan's Law.

So the surface area of Ori is 229,500 times greater than the surface area of the Sun. This star has a radius (remember area is proportional to R²) which is 479 times larger than the Sun. 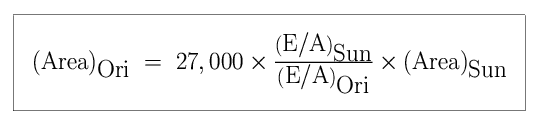Ori is cool, but large.

Let's revisit Stephan's Law, given what we now know.

E
= sigma × T

4 × R

E = (4 sigma ) × R T

L = (4 sigma ) × R T

The energy, E, emitted by a star (equivalent to the luminosity, L) is proportional to the square of the radius, R, and the fourth power of the temperature, T. We can express these quantities as a ratio between the properties of two stars:

L
= (4 sigma ) × R T

L (4 sigma ) × R T

L
= R
× T

L R T

If star A is twice as hot as star B, but emits the same total amount of energy, is it larger or smaller? By how much?
If star A is 625 times as luminous (emits 625 times as much energy) as star B, but the same size, is it hotter or colder? By how much?
If the radius of a star quadrupled in size and the energy output stayed constant, would it get hotter or colder? By how much?
If a white dwarf star had a temperature of 20,000K, would it be brighter or fainter than the Sun?

By making one of the two stars the Sun, we can express the properties of any star in solar units.

L
= R
× T

L R T

If a star is twice as hot as the Sun, with solar luminosity, what is its radius in solar units?
If a star is 625 times as luminous as the Sun, and the same size as the Sun, what is its temperature in solar units?
If a star is four times as large as the Sun, with solar luminosity, what is its temperature in solar units?
If a star has one-hundredth solar luminosity and is 5 times hotter than the Sun, what type of star is it?
If a star is ten-thousand times brighter than the Sun and is the same temperature as the Sun, what type of star is it?
What type of star is Ori?

Thanks to Mike Bolte (UC Santa Cruz) for the base contents of this slide.