What kind of stars are found here?

A star in this region of the Hertzsprung-Russell diagram has a temperature of roughly 3,700 kelvin (3,700 K), a luminosity 533,000 times more than that of the Sun (533,000 × LSolar), and a radius fifty-six times larger than the Sun (R = 56 × RSolar). This star lies in the region above the Main Sequence, where giant stars are found.

Try to read the values of L, T, and R for yourself from the diagram. Do you estimate values for the luminosity, temperature, and size of the star similar to those listed above?

Hertzsprung-Russell Diagram. The x-axis is labeled 'Surface Temperature' (in units of kelvins) with high temperatures around 60,000 on the left and low temperatures around 3,000 on the right. The points representing stars which appear furthest to the left are drawn in blue, those in the middle temperature range are drawn in yellow and orange, and those furthest to the right are drawn in red. The y-axis is labeled Luminosity (in units of solar luminosity), with low luminosities around 0.0001 at the bottom and high luminosities around 200,000 at the top. A third parameter, Radius (in units of solar radii), is also labeled. Lines of constant radius extend from the upper-left to the lower-right, covering the whole space with a set of parallel lines. In the lower-left corner we find the line labeled 'R is equal to 0.001 solar radii'; successive lines are labeled 0.01, 0.1, 1, 10, 100, and 1,000 solar radii, with the line for 'R is equal to 1,000 solar radii' being located in the upper-right corner. A series of blue, yellow, and orange points scattered along the 'R is equal to 0.01 solar radii' line is made up of white dwarf stars. A large set of red (and a few yellow and orange) points made up of giant stars appears between the 1 and 1,000 solar radii lines. The 1 solar radii line extends from the upper-left corner to the lower-right corner. The Main Sequence (a curved sequence of blue, yellow, orange, and red points) mainly follows the 0.1 to 10 solar radii lines; at the high luminosity end it curves up to slightly higher luminosities and at the low luminosity end it curves down to slightly lower luminosities. In addition, there are three green lines on the figure which intersect around the point near to 3,700 kelvins and 533,000 solar luminosities. One points down to the x-axis, one points left to the y-axis, and one is parallel to the black lines of constant radius (being drawn at a radius of around 56 solar radii).

If we doubled the radius of a star in this region, and held its brightness (luminosity) constant, how would its temperature change?

We can answer this question by beginning with the Stefan-Boltzmann Law, relating the temperature (T), size (R), and luminosity (L) of a star to each other. Measuring L, R, and T in solar units, we say that:

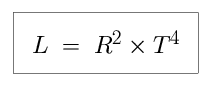
Equation: L is equal to R-squared times T-raised to the fourth power

We begin by solving the Stefan-Boltzmann equation for T. (We need to have T alone, on the left hand side of the equation.) Dividing both sides of the equation by R2,

Equation: T-raised to the fourth power is equal to L, divided by R-squared

The next step is to take the fourth root of each side of the equation:

Equation: The fourth root of T-raised to the fourth power is equal to T, which is equal to the fourth root of ( L, divided by R-squared ), which is equal to the fourth root of L, divided by the square root of R

Now that we have an expression for T in terms of L and R, we can calculate the temperature in each case. The first case is quite simple.

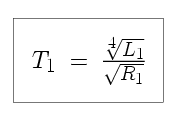
Equation: T_1 is equal to the fourth root of L_1 divided by the square root of R_1.

We now double the radius of the star, and examine the change in the temperature. For the second case,

Equation: T_2 is equal to the fourth root of L_2 divided by the square root of R_2, which is equal to the fourth root of L_2 divided by the square root of ( 2 times R_1 ), which is equal to the fourth root of L_1 divided by the square root of R_1 divided by the square root of 2, which is equal to T_1 divided by the square root of 2, which is equal to 0.707 times T_1.
By doubling the stellar radius and holding the luminosity constant, we have forced the temperature to decrease by almost 30%! The star cannot maintain as high a temperature across the enlarged surface without pumping out more energy.