What kind of stars are found here?

A star in this region of the Hertzsprung-Russell diagram has a temperature of roughly 7,000 kelvin (7,000 K), a luminosity 17,000 times more than that of the Sun (17,000 × LSolar), and a radius eighty-four times larger than the Sun (R = 84 × RSolar). This star lies in the region above the Main Sequence, where giant stars are found. The high luminosity indicates that this supergiant star was a hot, high mass star when it lived on the Main Sequence.

Try to read the values of L, T, and R for yourself from the diagram. Do you estimate values for the luminosity, temperature, and size of the star similar to those listed above?

Hertzsprung-Russell Diagram. The x-axis is labeled 'Surface Temperature' (in units of kelvins) with high temperatures around 60,000 on the left and low temperatures around 3,000 on the right. The points representing stars which appear furthest to the left are drawn in blue, those in the middle temperature range are drawn in yellow and orange, and those furthest to the right are drawn in red. The y-axis is labeled Luminosity (in units of solar luminosity), with low luminosities around 0.0001 at the bottom and high luminosities around 200,000 at the top. A third parameter, Radius (in units of solar radii), is also labeled. Lines of constant radius extend from the upper-left to the lower-right, covering the whole space with a set of parallel lines. In the lower-left corner we find the line labeled 'R is equal to 0.001 solar radii'; successive lines are labeled 0.01, 0.1, 1, 10, 100, and 1,000 solar radii, with the line for 'R is equal to 1,000 solar radii' being located in the upper-right corner. A series of blue, yellow, and orange points scattered along the 'R is equal to 0.01 solar radii' line is made up of white dwarf stars. A large set of red (and a few yellow and orange) points made up of giant stars appears between the 1 and 1,000 solar radii lines. The 1 solar radii line extends from the upper-left corner to the lower-right corner. The Main Sequence (a curved sequence of blue, yellow, orange, and red points) mainly follows the 0.1 to 10 solar radii lines; at the high luminosity end it curves up to slightly higher luminosities and at the low luminosity end it curves down to slightly lower luminosities. In addition, there are three green lines on the figure which intersect around the point near to 7,000 kelvins and 17,000 solar luminosities. One points down to the x-axis, one points left to the y-axis, and one is parallel to the black lines of constant radius (being drawn at a radius of around 84 solar radii).

How can we find the exact luminosity L of a star in this region of the Hertzsprung-Russell diagram, if we know its temperature T and its radius R?

We can use the Stefan-Boltzmann Law to relate the temperature (T), size (R), and luminosity (L) of a star to each other. Measuring L, R, and T in solar units, we say that:

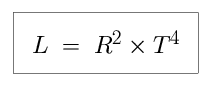
Equation: L is equal to R-squared times T-raised to the fourth power

Let us say that the temperature of the star is exactly 7,200 K. We know that the temperature of the Sun is 5,800 K, so we can convert the temperature of the star into solar units. This is just a way of asking How hot is the star relative to the Sun? (If the star is twice as hot as the Sun, for example, T = 2 × TSolar. If the star is half as hot as the Sun, T = 0.5 × TSolar.)

Equation: T is equal to 7,200 K, which is equal to ( 7,200 K divided by 5,800 K ) in units of solar temperature, which is equal to 1.24 in units of solar temperature (1.24 times hotter than the Sun).

This star is one and a quarter as hot as the Sun. Now assume that the radius of the star is exactly 84.4 × RSolar. (We don't need to convert this radius to solar units, as we are already using them.) The final step is to calculate the luminosity L, from T and R.

Equation: L is equal to 84.40-squared times 1.24-raised to the fourth power, which is equal to 16,900 in units of solar luminosity (16,900 times more luminous than the Sun).

We estimated a similar value of L = 17,000 LSolar from the diagram – so we did a good job working with our eyes!