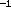
 meters) to each other that the
short-range but very strong nuclear attractive force will
bind or fuse the protons together.
meters) to each other that the
short-range but very strong nuclear attractive force will
bind or fuse the protons together.
There is another way to derive energy from atomic nuclei. Think about a gas of
protons. The pressure exerted by the gas increases as the temperature of the
gas increases. If you think about a container filled with gas atoms or
molecules, the thermal pressure exerted on the walls of the container is due
to all the atoms and molecules bouncing off the walls. Remember, temperature
is just a measure of the mean kinetic energy of the gas particles. At
low temperatures, the electrical repulsion between them prevents the
close approach of any two protons. But as the temperature of the gas
increases in the core of the Sun, the minimum approach distance decreases, and
occasionally two protons approach close enough (10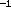
 meters) to each other that the
short-range but very strong nuclear attractive force will
bind or fuse the protons together.
meters) to each other that the
short-range but very strong nuclear attractive force will
bind or fuse the protons together.
 |
| [NMSU, N. Vogt] |
When two protons fuse, a chargeless, perhaps massless, particle called a
neutrino (
 ) is spit out, and one of the protons
emits an anti-matter particle called a positron (e
) is spit out, and one of the protons
emits an anti-matter particle called a positron (e ) – like a
positively charged electron. Having lost its electrical charge, the proton
becomes a neutron. The shorthand for this reaction is:
) – like a
positively charged electron. Having lost its electrical charge, the proton
becomes a neutron. The shorthand for this reaction is:
 H H + +
 H H

 H H +
e +
e + +
 
|
There is a short string of similar reactions that go on in any hot gas of hydrogen atoms. This is called the proton-proton cycle or the P-P cycle. Four protons are combined to form a helium atom, with by products of two positrons, two neutrinos, and released energy in the form of gamma rays.
| Step I: |  H H + +
 H H |
 |
 H H +
e +
e + +
  |
| Step II: |  H H + +
 H H |
 |
 He He + +
 |
| Step III: |  He He + +
 He He |
 |
 He He + +
 H H + +
 H H + +
 |
The whole process can be summarized as one net reaction:
4  H
H

 He
He + 2
e
+ 2
e + 2
+ 2
![]()
 +
Energy (
+
Energy (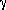 )
)
 |
| [NMSU, N. Vogt] |
Here is the amazing thing about the fusion process:
| Mass (4H) | = | 6.6943 × 10  grams grams |
Mass ( He He + 2 e + 2 e + 2 + 2
  ) ) |
= | 6.6466 × 10  grams grams |
The difference in masses means that 0.048 × 10
 grams of matter disappear in the P-P
Chain. This mass has been converted into energy (gamma rays). For one
reaction, the energy released is:
grams of matter disappear in the P-P
Chain. This mass has been converted into energy (gamma rays). For one
reaction, the energy released is:
| E | = | 0.048 × 10  |
grams × c |
= | 4.8 × 10  |
grams × c |
= | 4.8 × 10  |
grams × (3 × 10  )
) cm
cm /
sec /
sec |
= | 4.3 × 10 |
grams cm /
sec /
sec |
| = | 4.3 × 10 |
ergs |
How much energy is contained within an erg?
 (10,000) ergs to raise your pen 1 centimeter above your desk,
fighting against the Earth's gravity.
(10,000) ergs to raise your pen 1 centimeter above your desk,
fighting against the Earth's gravity.
 ergs will power a light-bulb for one second.
ergs will power a light-bulb for one second.

 ergs per second.
ergs per second.
For every 4 hydrogen atoms (6.7 × 10
 grams) we get this much energy out
of the reaction, so we can calculate the efficiency of the P-P Chain, and
compare it to the efficiency of coal power and gravitational potential energy:
grams) we get this much energy out
of the reaction, so we can calculate the efficiency of the P-P Chain, and
compare it to the efficiency of coal power and gravitational potential energy:
6.4 × 10  |
ergs/gram | from the P-P Chain |
1 × 10  |
ergs/gram | from GPE conversion |
4 × 10  |
ergs/gram | from chemical burning |