- how much energy is produced and radiated by the star;
- the scale of objects in the Galaxy, and the scale of the Galaxy itself.
The intrinsic luminosity of a star, the amount of energy it emits, does not change with distance. The apparent luminosity, how bright it appears, does. More distant stars appear fainter to us, and the further a star lies from Earth, the fainter it will appear to us in our telescopes.
Think about the photons emitted by a star, which radiate in all directions.
If you enclosed a star in a sphere with a radius twice that of the star, you
could count the total number of photons which passed through the sphere per
second. If you placed a second sphere at four stellar radii, the same number
of photons would pass through it per second (there is nowhere else for them
to go). The surface area of a sphere of radius R is
4
×R×R, so it scales with
R squared. If the surface area of the sphere increases with the square
of the radius, and the number of photons which pass through each sphere is
constant, then the density of the photons, and thus the apparent brightness,
must decrease with the square of the radius, or the square of the distance
to the source of the light.
The apparent luminosity of a star scales with the square of its distance, so a star which is placed twice as far away will appear one-fourth as bright, and a star which is three times further away will appear nine times fainter.
|
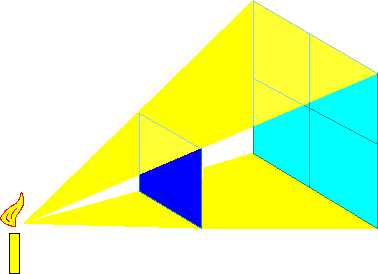
| [NMSU, N. Vogt] |
Just as a star placed twice as close to us will appear four times brighter, a star or planet placed twice as close to us will appear twice as wide, and twice as tall (or, more simply, we can say that the apparent radius will appear to double).
|
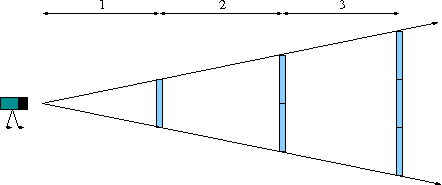
| [NMSU, N. Vogt] |