 |
One of the key questions of astronomy is how far away objects are. When we observe a bright star or galaxy, we need to distinguish between objects which appear bright just because they are near to us and those which are far away and yet so intrinsically bright that they outshine nearer objects. Likewise, we need to know whether objects are intrinsically small, and which appear small because they are so far away from us.
How do we measure the distance to astronomical objects beyond the solar system? The nearest star is so far away that it takes even light more than four years to travel from here to there, so a surveying journey is out of the question.
The idea of parallax is very simple, and yet very powerful. Hold your arm out at eye height, and focus on your thumb. Now take turns closing first one eye, and then the other. Your thumb will appear to jump from side to side against a background wall, simply because you are looking at it from two different positions (separated by the bridge between your two eyes). If you slowly bring your thumb closer to you, you will see it appear to move further and further as you switch eyes (shifting by a larger and larger angle in your field of view). The shift in the position of your thumb is largest when your thumb is closest to you, and decreases as you move your thumb away from your body.
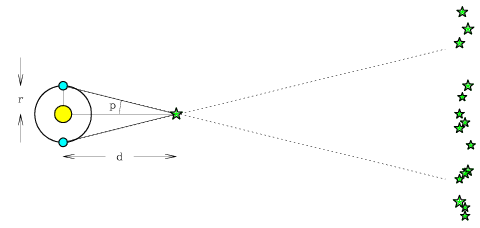
Astronomers use the same trick to judge the distance to nearby stars. Just as your eyes are separated by a few inches, we need to take observations with telescopes that are as far apart as possible, or take repeated observations through a single telescope that moves over a large distance. Because the Earth rotates once around the Sun at a (large) distance of 1 A.U. (150 million kilometers) each year, by taking observations over a six month period we can cause our telescope to shift in position by 300 million kilometers, twice the radius of the Earth's orbit.
In the figure below, see how the position of a nearby star appears to change against the background panorama of distant stars, as the Earth moves from January to July, and back.
 |
 |

The best parallax measurements to date come from the Hipparcos satellite, which orbited the Earth high above the turbulent atmosphere and made very accurate measurements of the positions of stars (and the parallax angle, or how those positions changed over the course of a year). Hipparcos was able to measure parallax angles to within 0.001 arcseconds for over 100,000 stars. It determined p to within 1% for 400 stars within 30 light-years of Earth, and to within 10% for another 27,000 stars extending out as far away as 300 light-years.
What happens to p if the star is further away? We can see that as the distance d to the star increases, the parallax angle decreases. For the nearest stars like Alpha Centauri, p is less than an arcsecond (0.77 arcseconds), and it is even less than that for all other stars in other solar systems. Parallax can thus be used to measure the distances only to relatively nearby stars, those close enough that the change in their angular position over six months is larger than the sensitivity of our measurement of that angle.
 |
 |