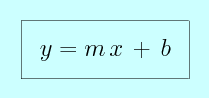
Good science depends critically upon solid data analysis. Let's look at an example of this, by considering functions that can be fit with a straight line. If we know the relationship between two variables x and y, then if we know x we can predict the value of y. (The values for y and x could be anything – peak temperature versus day of the year, lunar phase versus day of the lunar month, height versus age, ...).
If you know the position of two points in space, there is one and only one line which will pass through them both. (Test this idea for yourself, by marking two points on a piece of paper and trying to draw two different straight lines through them.) We can say that these two points are defined by their x and y coordinates (x,y), their location to the left or right (x) and upwards or downwards (y) of a starting point, or origin.
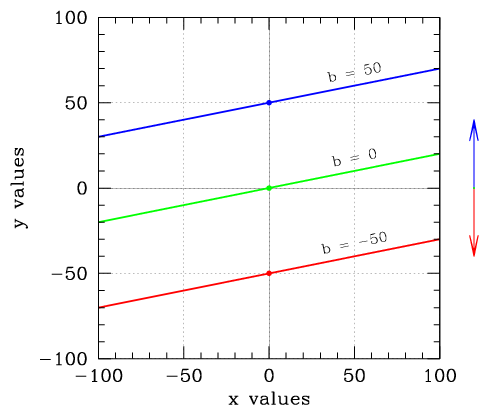
We often define a line in terms of two variables. The first is its slope, the amount by which its position increases in y as we increase x, often called m. The second is its y-intercept, the y coordinate along the line for which x is equal to zero, called b.
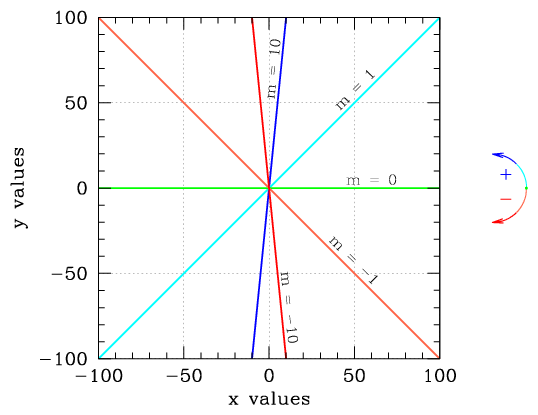
The slope of a line tells you how tilted it is. The larger its slope, the more a line tends toward a pure vertical, while a line with a slope of zero is a horizontal line. A line with a large, negative slope also tends toward a vertical, but descends rather than ascending. This figure shows five different lines (each one drawn in a different color). The bluer the line, the higher the slope, and as the lines shift toward redder colors, the slopes shift down toward negative infinity.
|
|
 y, or y2 - y1),
divided by the change in x (
y, or y2 - y1),
divided by the change in x ( x, or x2 - x1).
x, or x2 - x1).
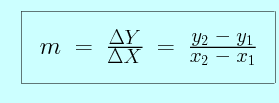


When we fit a line to a set of data points, we define the root mean square (rms) deviation of the line as a quantity built by combining the deviation (the offsets) of each of the points from the line. The higher the rms value for a fit, the more poorly the line fits the data (and the more the points lie off of the line).