 is the angle the
Earth rotates through during this time interval
is the angle the
Earth rotates through during this time interval
 T.
T.
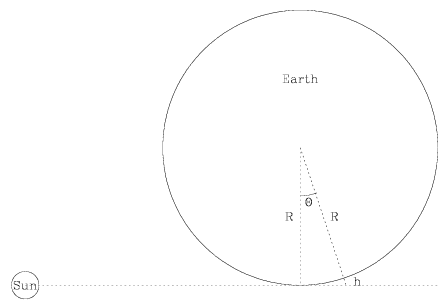
We can measure the radius of the Earth for ourselves, using nothing but a watch!
At sunset, measure the amount of time between which the Sun appears to set
from the ground level and from the height of your head (h). When you
are standing up, you can "see a little further around the corner" and the Sun
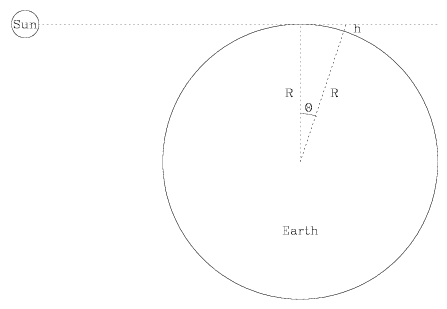
takes a little bit longer to set. This picture shows the Earth and the Sun,
looking down on the solar system from the top of the North Pole. The Earth is
rotating counter-clockwise, so the Sun sets first at ground level and then
later at head height. The radius of the Earth is identified as a distance
R, and  is the angle the
Earth rotates through during this time interval
is the angle the
Earth rotates through during this time interval
 T.
T.
 |
| [NMSU, N. Vogt] |
At sunrise, measure the amount of time between which the Sun appears to
rise from the height of your head (h) and from the ground level. When
you are standing up, you can "see a little further around the corner" and the
Sun rises a bit sooner. This picture shows the Earth and the Sun, looking
down on the solar system from the top of the North Pole. The Earth is
rotating counter-clockwise, so the Sun rises first at head height and then
later at ground level. The radius of the Earth is identified as a distance
R, and  is the angle the
Earth rotates through during this time interval
is the angle the
Earth rotates through during this time interval
 T.
T.
 |
| [NMSU, N. Vogt] |
Here is the relationship between your height h, the time interval
 T, and the radius of the
Earth R, where R and h are measured in centimeters,
T, and the radius of the
Earth R, where R and h are measured in centimeters,  T is measured in seconds, and
T is measured in seconds, and
T/240 is in units of
degrees.
![Equation for R, the radius of the Earth. R is equal to h times the cosine of ( Delta-T over 240 ) divided by the quantity [ 1 minus cosine of ( Delta-T over 240 ) ].](math/eqn01.png) |
Here are the results for various intrepid members of a previous class who performed the experiment.
 T (seconds) T (seconds) |
h (cm) | R (108 cm) |
|---|---|---|
| 45 | 180 | 0.3 |
| 27 | 163 | 0.8 |
| 14 | 152 | 2.9 |
| 11 | 147 | 4.7 |
| 12 | 178 | 4.8 |
| 8 | 160 | 9.4 |
People have measured the radius of the Earth in detailed ways and found it to be 6.4 × 108 centimeters. We did pretty well!