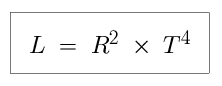
We have an equation with three variables (L, R, and T). If we know the
value of two of the variables, we can solve for the value of the third.
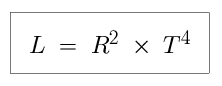 |
If R is equal to two (R = 2) and T is equal to six (T = 6), what is the value of L?
 |
We can also describe the relationship between L, R and T in terms of proportions (if we change R and T, what will be the effect on R)?
We know that if R squared, or R × R, increases, so will R. Similarly, if T raised to the fourth power, or T × T × T × T, gets smaller, so will T. We can say that L is equal to R squared × T raised to the fourth, and L is proportional to R × T.
 |
