F = GMm/r²

Where G is the gravitational constant, M is the mass of the more massive body (Jupiter), m is the mass of the less massive body (Europa), and r is the distance of the two bodies. It can be seen that as the distance between the two bodies decreases, the force increases as r², and as the mass of the bodies increase the force also increases.

Tidal force is the differential gravitational force felt across a body. Since the front face of Europa is closer to Jupiter than the far side, it will feel a greater gravitational force. The magnitude of force felt on the side of Europa facing Jupiter is:

F_front = GMm/r²

The force felt on the side facing away from Jupiter is:

F_back = GMm/(r+d)²

where d is the diameter of the moon. The difference in these two forces is the tidal force felt across Europa:

F_tidal = 2GMmd/r³

It can be seen that larger moons have greater tidal forces across them. However, it is not tidal force alone that causes tidal heating within a body. In order for heating to occur, the tidal force must change. This can be imagined if you take a rubber band and stretch it repeatedly. A band that is stretched and left stretched will not generate heat. However, if the band is repeatedly stretched and flexed, heat will be generated. This is becuase stretching and flexing induce frictional heating, similar to rubbing your hands together on a cold day. There is enough tidal heating occurring in Europa to keep its interior warm and the moon to stay geological activity, even though it is smaller than our own Moon.

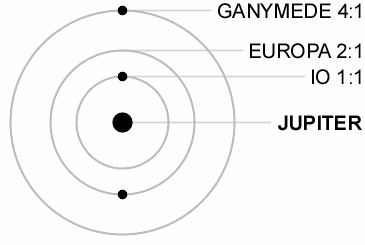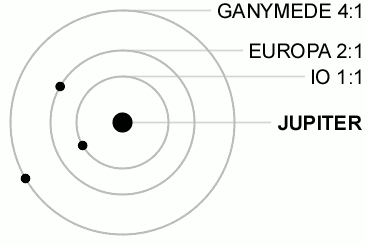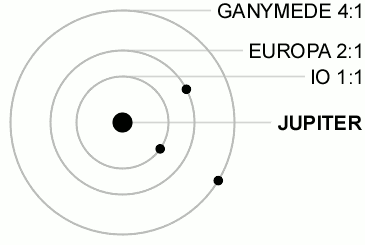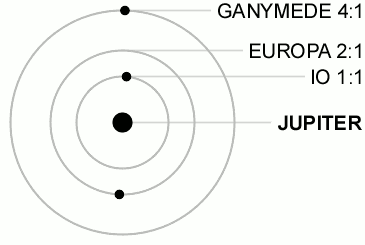
The change in tidal force (also known as tidal stress) occurs because of the orbits of Io, Europa, and Ganymede. Table 1 shows that the first three Galilean moons are locked in a 4:2:1 orbital resonance. For every orbit Ganymede completes, Europa completes two and Io completes four. This is illustrated in the diagram below (Figure 4). This resonance forces Europa to have an eccentricity of e = 0.01 (Greenberg 1981, Peale 1986). Eccentricity is a measure of how much an orbit deviates from a perfect circle. A perfect circle has an eccentricity of 0, an elliptical orbit has an eccentricity between 0 < e < 1, e = 1 is a parabolic orbit, and e > 1 is a hyperbolic orbit. Since Europa does not have a perfectly circular orbit, its distance from Jupiter changes. This causes a change in the tidal force on the moon. In addition, Io and Ganymede change their distance with respect to Europa and also introduce a tidal stress.

Figure 4. Orbital Resonances of Io, Europa, and Ganymede.

Europa is locked into a synchronous rotation around Jupiter, just like our Moon is around the Earth. For every revolution Europa makes around Jupiter it also completes one rotation. It has a 3.55 day orbital period and rotation period, so the same side of Europa always faces Jupiter. Thus, is makes one revolution around Jupiter every Europa day. The tidal stress experienced over one orbit is referred to as the "diurnal" stress. The changing tidal force induced by the eccentricity of Europa and tug from the other moons deforms Europa by as much as 3% each Europa day. (Greenly et al. 2004). Moore and Schubert (2000) calculate that this should result in a deformation anywhere between 1 m and 30 m depending on if the ice shell is solid down to the silicate layer or if the ice shell is thinner and sits above a liquid water layer. The dissipation of this strain heats the interior of the moon and flexing from the diurnal stress results in the geomorphic features seen across the surface.

Table 1

Satellite	Mass (x 1020)	Radius (km)	Density (g/cm3)	Distance from Parent Body (x 103 km)	Orbital Periods (days)
Io	893.3	1821.3	3.53	421.77	1.77
Europa	480	1565	3.02	671.08	3.55
Ganymede	1482	2634	1.94	1070.4	7.15
Callisto	1076	2403	1.85	1882.8	16.69
Our Moon	734.9	1736	3.34	384.40	27.32

^{From de Pater and Lissaure, 2nd Edition.}

Overview
Craters
Ridges
Bands
Chaos
Astrobiology
Bibliography